Educational DP 题解
这篇文章已经咕了一年了,原先的前言已经完全脱离时代了,在第一版到最终成文的期间过去了很多事情,趁现在毕业前夕有点时间迅速把坑给填了,也算是给大学和竞赛生涯画个句号吧。
这次的刷题对象是 AtCoder 的 Educational DP Round。从简单到困难的问题都有,倒挺适合我这种不会 DP 的人的。
我的题解习惯是不贴代码的,所以下面所有的都是关于题目的讲解和方程的推导,要看代码参考Github或者提交页面。
A. Frog 1
最基础的 DP 了吧,考虑到第 $i$ 格只有两种走法,则最小花费就是这两种里面二选一就可以了啊。
转移方程就是: $$ \text{dp}[i] = \min\{\text{dp}[i-1]+|h_i-h_{i-1}|,\text{dp}[i-2]+|h_i-h_{i-2}|\} $$ 答案就是 $\text{dp}[N]$。$\mathcal{O}(N)$ 时间递推过去就可以了。
B. Frog 2
这个 DP 就是在上面扩展了一下,枚举一下距离就行。
转移方程: $$ \text{dp}[i] = \min_{1\le j\le k}\{\text{dp}[i-j]+|h_i-h_{i-j}|\} $$ 答案是 $\text{dp}[N]$。$\mathcal{O}(NK)$ 时间枚举一下就可以了。
C. Vacation
实际上不选择相同的活动我们可以这么来想:我们每次从两个没选过的活动里面选一个最大值就行。那么状态就应该是 $\text{dp}[i][0/1/2]$,$0,1,2$ 代表第 $i$ 天选择的活动的项目,具体怎么编码都可以。
那么转移方程就是: $$ \text{dp}[i][j] = \max_{0\le k\le2\land k\ne j}\{\text{dp}[i-1][k]\}+\text{score}[i][j] $$ 答案就是 $\max_{0\le k\le 2}\{\text{dp}[N][k]\}$。 复杂度 $\mathcal{O}(N)$。
D. Knapsack 1
模板 01 背包问题。设 $\text{dp}[i][j]$ 代表选了前 $i$ 件物品中体积为 $j$ 的最大价值。
转移方程: $$ \text{dp}[i][j] = \max\{\text{dp}[i-1][j], \text{dp}[i-1][j-w_i]+v_i\} $$ 答案是 $\text{dp}[N][W]$。复杂度 $\mathcal{O}(NW)$。
一个常见的省内存技巧是,注意到 $i$ 仅和上一轮,即 $i-1$ 有关,我们可以省略掉这一维,然后数组滚动使用即可。这样的要求是,我们需要倒序枚举体积:如果我们顺序枚举,那么我们更新的时候会使用 $i$ 轮去更新 $i$ 轮,就不是从 $i-1$ 轮更新过来了。这个观察应该还是比较自然的。
E. Knapsack 2
这个题好玩。由于总体积非常大 ($10^9$),我们在常规背包的技巧中经常使用的按体积 dp 价值就不行了。这个时候我们反着过来,考虑到总价值上限不大 ($10^5$),我们来这样 dp:看某个价值 $i$ 需要的最小体积。
$\text{dp}[i][j]$ 代表的就是对于前 $i$ 件物品,价格为 $j$ 的最小体积。那么,转移方程就应该这么写: $$ \text{dp}[i][j] = \min\{\text{dp}[i-1][j], \text{dp}[i-1][j-v_i]+w_i\} $$
最后的答案就是 $\max_{1\le i\le V}\{i\cdot[\text{dp}[N][i]\le W]\}$。复杂度是 $\mathcal{O}(NV)$ 的。常用的倒序枚举一维滚动优化是不变的,只是第二层的上限从体积变成了总价值。
F. LCS
模板最长相同子序列问题。设 $\text{dp}[i][j]$ 代表序列 $s[1..i]$ 和序列 $t[1..j]$ 的最长相同子序列的长度,考虑 $s[i]$ 和 $t[j]$:
- 假如 $s[i]=t[j]$,那么证明当前字符参与 LCS 的构建。
- 否则,最长的 LCS 应该是我们从这两个字符中选择能带来较大 LCS 那个。
所以,转移方程就应该是: $$ \text{dp}[i][j]=\begin{cases} \text{dp}[i-1][j-1]&,s[i]=t[j] \\\max\{\text{dp}[i][j-1], \text{dp}[i-1][j]\}&,s[i]\ne t[j] \end{cases} $$ 答案就是 $\text{dp}[N][M]$,其中 $N, M$ 分别是序列 $s$ 和 $t$ 的长度。复杂度 $\mathcal{O}(NM)$。
这题比较麻烦的是找出这个 LCS。这里我们的技巧叫做 正着 DP,倒着搜索 。意思就是,我们先正着把这个答案 dp 出来,然后我们从 $\text{dp}[N][M]$ 出发去找答案:由于参与到 LCS 构建的字符一定满足 $\text{dp}[i][j] = \text{dp}[i-1][j-1]+1$,那么我们就倒着去测试是否某个点满足这个条件即可,否则贪心往 $\text{dp}[i-1][j], \text{dp}[i][j-1]$ 这里面等于 $\text{dp}[i][j]$ 的那个搜过去。
G. Longest Path
DAG 上的 DP。很直观的来说,我们需要找到最长路,每次一定要从某个起点出发,所以我们可以先拓扑排序一下,然后逐个 dp 就可以了。容易观察到的是,这两个过程并不冲突,所以我们完全可以合并在一起,一边拓扑排序一边 dp。
设 $\text{dp}[v]$ 代表从以节点 $v$ 为终点的最长路的长度,那么转移方程就应该是: $$ \text{dp}[v] = \max_{1\le u\le n\wedge<u,v>}\{\text{dp}[u]\}+1 $$ 答案自然就是 $\max_{1\le i\le N}\{\text{dp}[i]\}$。复杂度就是拓扑排序的复杂度,$\mathcal{O}(N+M)$。实现应该还有一些细节需要考虑一下。
H. Grid
模板题。设 $\text{dp}[i][j]$ 是从 $(1,1)$ 走到 $(i,j)$ 的方案数,那么:
- 如果 $(i,j)$ 不可达,自然就是 $0$。
- 否则,只能从 $\text{dp}[i-1][j]$ 和 $\text{dp}[i][j-1]$ 两格中的某一格过来。
所以,转移方程就是: $$ \text{dp}[i][j]=\begin{cases} 0&,(i,j)\text{ is not reachable} \\\text{dp}[i-1][j]+\text{dp}[i][j-1]&,\text{otherwise} \end{cases} $$ 答案就是 $\text{dp}[H][W]$,记得一步一模。复杂度 $\mathcal{O}(HW)$。
I. Coins
概率 DP。我们设 $\text{dp}[i][j]$ 代表有 $i$ 个硬币是正面,$j$ 个硬币是反面的概率,那么这个状态其实也并不难想。
多了一枚硬币的情况有两种:
- 多了一枚正面硬币,这是从 $\text{dp}[i-1][j]$ 的情况过来的。
- 多了一枚反面硬币,这是从 $\text{dp}[i][j-1]$ 的情况过来的。
又由于上面的所有情况都只会少 1 枚硬币,这也就提示我们,可以按硬币数来 dp:枚举当前局面有多少硬币,然后对所有可能的 $i, j$ 情况做讨论即可。由于我们自然从上一轮带过来的,所以我们滚动少了一个维度。
那么,假设当前局面有 $m$ 枚硬币,有 $i$ 枚硬币是正面,我们很容易得到如下的转移方程: $$ \text{dp}[i][m-i] = \text{dp}[i-1][m-i]\cdot p_m + \text{dp}[i][m-i-1]\cdot(1-p_m) $$ 这样的话,针对每一个 $m$ 枚举 $i$ 即可。容易观察到上述过程是 $\mathcal{O}(N^2)$ 的。
最终答案就是 $\sum_{\frac{N}{2}\le i\le N}\text{dp}[i][N-i]$。
J. Sushi
期望 DP。考虑当前有 $a$ 盘寿司有 $1$ 个,$b$ 盘有 $2$ 个,$c$ 盘有 $3$ 个,那么 $\text{dp}[a][b][c]$ 就是所求的期望,答案就是 $\text{dp}[cnt_1][cnt_2][cnt_3]$。接下来考虑转移:设 $d=a+b+c$,考虑投骰子,投到 $a,b,c$ 的概率就是 $\frac{a}{d}, \frac{b}{d},\frac{c}{d}$,乘一下数就可以了。而投到这 $d$ 面的期望次数等于 $\sum_{k=1}^\infty k(\frac{n-d}{n})^{k-1}\frac{d}{n}$,显然就是 $\frac{n}{d}$。根据期望的线性性,把它们全部加起来就可以了。
那么转移方程就是: $$ \text{dp}[a][b][c] = \frac{n}{d} + \text{dp}[a-1][b][c]\cdot\frac{a}{d}+\text{dp}[a+1][b-1][c]\cdot\frac{b}{d}+\text{dp}[a][b+1][c-1]\cdot\frac{c}{d} $$ 复杂度是 $\mathcal{O}(N^3)$。实现就 dfs 记忆化算一下就行了。
K. Stones
完蛋,博弈论。老外是不是很喜欢把所有和递推有关的题目不管带不带子问题重合都叫做 DP 啊?
现学现卖的 SG 定理和函数啊。SG 定理说的是,某个游戏的 SG 函数等于各个子游戏的 SG 函数的 Nim 和。先分清两个概念,对于 $\text{SG}(x)$,我们指的是对于局面 $x$ 的函数值,而对于 $\text{SG}(G)$,我们指的是游戏 $G$ 的函数值。假设游戏 $G$ 的初始状态是 $x_G$,那么可以简单理解为 $\text{SG}(G) = \text{SG}(x_G)$。那么显然,对于游戏 $G=\sum_{i=1}^pG_i$,$\text{SG}(G)=\bigoplus_{i=1}^p\text{SG}(G_i)$。
下面是一些基础知识:首先是在双方都最理智的操作下,我们的必胜点就是当前局面一定能导向当前操作的人是必胜的,必败点相反。容易观察的是,对于无偏组合游戏,我们的胜负仅和当前的局面有关,而和操作人和操作顺序等无关。那么我们有以下三条定理:
- 所有的终结点都是必败点。
- 必胜点至少有一个后继为必败点。
- 无论如何操作,所有必败点的后继都是必胜点。
第一个理解是显然的,由于存在无法进行任何操作的点,此点同样也就是必败点。后两个的理解比较麻烦,找点专业的书讲的肯定比我好。
下面就是 SG 函数的定义。$\text{SG}(x) = \text{mex}(S)$。$S$ 是 $x$ 的所有后继局面 SG 函数值的集合,$\text{mex}$ 运算是不属于这个集合的最小非负整数,如 $\text{mex}({0,1,2,4})=3,\text{mex}({2,3,5})=0$。显而易见的是,对于一个无法操作的状态 $p$,显然是必败态,则 $\text{SG}(p)=0$。同时我们也有,所有 $\text{SG}(x)=0$ 的局面 $x$ 都是必败状态。
具体求 SG 函数的话大概就是对每一个后继状态的 SG 函数值打一个 vis 标记,然后找到第一个没有 vis 标记的值。这个简单的子问题要枚举要 dfs 要二分就看大家各显神通了。同时打表找规律也是个办法。
那么这个题其实就很简单了,由于可选的后继状态和当前剩余的石子数量正相关,我们从小开始递推就可以了,每一个去分解 $x-a_i$ 然后求出所有的 SG 函数值最后对 $K$ 的询问做出回答就行。显然对于每一个 $i\le K$,需要枚举每一堆可选石子,所以复杂度 $\mathcal{O}(NK)$。
L. Deque
区间 DP + 记忆化搜索。题目虽然没说明,但是在 Sample 里面说明了是 Taro 先开始操作的。我们考虑 $\text{dp}[l][r][0/1]$,代表选择区间 $[l,r]$,当前操作的人是 $0$ 或者 $1$ 的最优 $X-Y$。如果我们编码 $0$ 是 Taro 的话,那么答案就是 $\text{dp}[1][N][0]$。
那么来推方程:
- 假如 $l=r$,那么根据当前的操作人,加减一下 $a_l$ 就可以了。
- 假如 $l\ne r$,那么我当前的操作就是选择 $[l+1,r]$ 或者 $[l, r-1]$ 然后加上或者减去端点的值,根据策略取一下大小值就可以了。
所以转移方程就是: $$ \text{dp}[l][r][cur]=\begin{cases} a_l&,l=r,cur=0 \\-a_l&,l=r,cur=1 \\\max\{\text{dp}[l+1][r][0]+a_l, \text{dp}[l][r-1][0]+a_r\}&,l\ne r,cur=0 \\\min\{\text{dp}[l+1][r][1]-a_l, \text{dp}[l][r-1][1]-a_r\}&,l\ne r,cur=1 \\\end{cases} $$ 考虑每个区间都会被枚举到,所以总复杂度是 $\mathcal{O}(N^2)$ 的。由于大区间是依赖于子区间的,实现的时候可以 dfs 下去,然后记忆一下就可以了。
M. Candies
做的时候不知道自己在想什么,实际上是个简单 DP。
设 $\text{dp}[i][j]$ 代表分配了前 $i$ 个糖果,总共分配了 $j$ 个糖果的方案数,答案就是 $\text{dp}[N][K]$。
下面来考虑转移。容易观察到的是,$\text{dp}[i][0]=1$,因为只有前面的所有轮都分配了 $0$ 个糖果才能到这个状态,自然只有 1 种方案。而对于 $j\ge1$ 的方程: $$ \text{dp}[i][j] = \sum_{p=1}^{\min\{a_i,j\}}\text{dp}[i-1][j-p] $$ 显然可以看出来后面的这个东西就是一个简单的前缀和,直接每次 $\mathcal{O}(K)$ 的时间维护掉就可以了,这样转移的时候就少一个循环。
当然,前几个糖果那维可以滚动掉,懒得写了。复杂度 $\mathcal{O}(NK)$。
N. Slimes
应该是国内选手最熟的区间 DP 入门题吧,怎么给安排到 N 来了……
就是 NOI 1995 那题石子合并原题简化版。考虑 $\text{dp}[l][r]$ 代表合并区间 $[l,r]$ 的最小代价,那么答案自然就是 $\text{dp}[1][N]$。
转移方程比较简单,从区间长度来枚举,由于只能相邻合并,那么考虑某个区间 $[l,r]$,我们可以选择区间内的任何位置 $p$ 为切断点,代表我们选择把石子堆 $[l,p]$ 和石子堆 $[p+1,r]$ 合并,那么不难发现代价就是 $\text{dp}[l][p]+\text{dp}[p+1][r]+\sum_{i=l}^ra_i$。可以发现后面这个式子需要多次计算,求一个前缀和就可以了。
那么状态转移方程就是: $$ \text{dp}[l][r]=\min_{l\le p\le r}\{\text{dp}[l][p]+\text{dp}[p+1][r]\}+\sum_{i=l}^ra_i $$ 由于我们相当于在枚举 $l, r$ 的同时还要枚举 $p$,复杂度显而易见是 $\mathcal{O}(N^3)$ 的。
O. Matching
状压 DP。
我们考虑这么设计状态:$\text{dp}[i][j]$ 代表分配到男士 $i$ 且此时女士分配的方案是 $j$ 。那么这个方案的来源很简单:比如对于 $j=10010_{(2)}$,当前男士的分配方案自然可能会来自 $j=00010_{(2)}$ 或者 $j=10000_{(2)}$。也就是说,来自前一轮的这些方案的和,其中当前方案上选择了女士 k(j & (1 << k))且这位男士和这位女士可以配对(edge[i][k])。
所以转移方程就应该是: $$ \text{dp}[i][j] = \sum_{k \text{ in the choice} \wedge <i,k>}\text{dp}[i-1][j\oplus2^k] $$ 然后我们又发现,由于我们知道了 $j$,我们自然就知道了当前轮分配了几个人,所以 $i$ 轮完全没用,直接给滚动掉。然后就可以直接 dp 了,答案是 $\text{dp}[2^N-1]$,复杂度 $\mathcal{O}(N\cdot2^N)$。
P. Independent Set
树形 DP 裸题。
设计状态很简单,设 $\text{dp}[v][0/1]$ 代表节点 $v$ 为黑色/白色的方案数,从根 $\text{rt}$ dfs 下去,答案就是 $\text{dp}[\text{rt}][0] + \text{dp}[\text{rt}][1]$。
转移的话也比较简单: $$ \text{dp}[v][c]=\begin{cases} \prod_{u\in\text{son}(v)}\text{dp}[u][1],&c=0 \\\prod_{u\in\text{son}(v)}(\text{dp}[u][0]+\text{dp}[u][1]),&c=1 \end{cases} $$
直接从 1 dfs 就可以了。复杂度 $\mathcal{O}(N)$。
Q. Flowers
线段树/树状数组优化转移。
设 $\text{dp}[i]$ 代表以 $i$ 为结尾的花的序列的最大美丽度,那么转移方程是非常显然的: $$ \text{dp}[i]=\max_{1\le j<i}\{[h_j<h_i]\cdot\text{dp}[j]\}+a_i $$ 复杂度是显然的 $\mathcal{O}(N^2)$,明显会 TLE。但由于 $h_i$ 是 $1\sim n$ 的一个排列,那么可以用类似于树状数组求逆序数的方法:每次先查询 $1\sim h_i$ 的最大值 $m_i$,然后就有 $\text{dp}[i]=m_i+a_i$,然后再把 $\text{dp}[i]$ 的值更新到点 $h_i$ 上。
这个显而易见的观察是,我们更新了某个点 $h_i$,假如查询了点 $h_j$,如果这个 $h_i > h_j$,那么这个值只会出现在线段树的右侧,询问是不会求出这个值的。
所以用一棵维护区间最大值的线段树优化转移就行。由于树状数组维护的是区间前缀最大值,这里查询的也是区间前缀最大值,也可以用。复杂度 $\mathcal{O}(N\log N)$。
R. Walk
矩阵快速幂求有向图长度为 $k$ 条数的裸题。
考虑存在 $u\to v$ 和 $v\to w$ 这样的两条路径,那么把这个矩阵相乘一次之后,就会出现 $u \to w$ 这样的一条路,这条路的值根据矩阵乘法定义很容易得到就是前面两条路径的方案的乘积。
换个想法来说,这个过程类似于 Floyd:我们使用中心点考虑两个点之间的转移,也就是路径 $u\to v$ 可以通过所有的中转点 $k$ 转移过来,其中存在这样的路径 $u\to k$ 和 $k\to v$。
那么就是跑一下矩阵快速幂然后统计答案就可以了,复杂度 $\mathcal{O}(N^3\log K)$。
S. Digit Sum
数位 DP 模板题。
考虑定义 dfs(pos, rem, limit) 代表从高到低第 pos 位,余数为 rem 以及前一位是否到达了可取值的上限的状态,然后直接记忆化搜索就行。当且仅当 pos == -1 && rem == 0 的时候返回 1,否则 pos == -1 的时候返回 0。要注意的是初始状态 0 也会被记入,到最后答案需要减 1。
注意到余数不影响调用次数,总复杂度是 $\mathcal{O}(\log K)$ 级别的(如果有误或者有更好的的复杂度分析欢迎告诉我)。
T. Permutation
想了一会儿没想出来,上 cf 看了个题解,豁然开朗。这套题我最喜欢的题目之一。
我们考虑定义 $\text{dp}[i][j]$ 代表前 $i$ 个位置,我们使用 $1\sim i$ 的排列满足了要求,且最后一个数为 $j$ 的方案数,易得答案即 $\sum_{i=1}^n\text{dp}[N][i]$。
转移过程非常精彩:我们考虑 $\text{dp}[i+1][j]$,假如 $s[i]=<$,说明 $j$ 这个数必须要比上一个数的最后一位要大,但是我们的 $j$ 有可能之前用到过(比如 $i=10, j=7$,显然 $\text{dp}[10][7]$ 在前面是一个合法的答案),我们怎么避免这个情况呢?
注意到前面是一个 $1\sim i$ 的排列,如果我们以 $j-1$ 为分界线,把 $j-1$ 之后的数都加一,在不破坏整体的大小关系的情况下我们消除了 $j$,然后我们再把 $j$ 放到当前位置,我们就得到了 $i+1$ 这个排列!
所以,针对于 $s[i]=<$ 的情况,我们只需要对 $\text{dp}[i][k], 1\le k<j$ 求一个和就得到了 $\text{dp}[i+1][j]$ 的值;同理,对 $\text{dp}[i][k], j\le k\le i$ 的值求一个和就是 $\text{dp}[i+1][j]$ 在 $s[i]=>$ 的情况的值了(我们使用了等号,因为假定上一个数为 $j$,那么加一之后 $j+1>j$ 恒成立,也满足要求)。
所以,我们的转移方程非常简单:
$$ \text{dp}[i+1][j]=\begin{cases} \displaystyle{\sum_{k=1}^{j-1}\text{dp}[i][k]},&s[i]=< \\\displaystyle{\sum_{k=j}^{i}\text{dp}[i][k]},&s[i]=> \\\end{cases} $$
注意到后面的求和是两个连续序列,直接前缀和每次 $\mathcal{O}(N)$ 维护掉则下一轮就可以 $\mathcal{O}(1)$ 转移了,总复杂度 $\mathcal{O}(N^2)$。可以看出 $\text{dp}$ 的第一维可以滚动掉,整个内存开销也变得非常小了。代码写出来也非常短。
U. Grouping
状压 DP。一开始自己把自己给关了,实际上思路是对的。
令 $mask_{(2)}$ 中为 $1$ 的位代表已经选了的兔子,$\text{dp}[mask]$ 为 $mask$ 下的答案,$\text{score}[mask]$ 为 $mask$ 的兔子全为一组时的分数。
转移应该是比较简单的:我们首先算出来某一个 $mask$ 下的分数,并令 $\text{dp}[mask]=\text{score}[mask]$。接下来我们枚举 $mask$ 的子集,考虑某一个子集拿出来为单独的一组,看看能不能提高得分即可。所以转移方程是:
$$ \text{dp}[mask]=\max\{\text{score}[mask], \max_{submask\subset mask}\{\text{dp}[mask\oplus submask]+\text{score}[submask]\}\} $$
$mask$ 从 $1$ 枚举到 $2^N-1$ 即可。转移过程中需要算一下得分或者 $\mathcal{O}(N^22^N)$ 预处理出来。答案为 $\text{dp}[2^N-1]$。
复杂度的分析比较奇妙。我们考虑一下需要的转移过程,易知 $\{(mask, submask)\}$ 构成了转移的状态集合,这个集合的大小就是最终的转移次数。考虑对于任意一对 $(mask, submask)$,在某一位上有下面三种情况:
- 这一位同为 $1$:代表我们选择将这只兔子绑定到其他组。
- 这一位 $mask$ 为 $1$ 而 $submask$ 为 $0$:代表这只兔子留在这一组内,我们选择其他的兔子拿出来构成新的组。
- 这一位同为 $0$:在原始方案下这只兔子就没有选。
由于每一位都是三种状态任选一种,总计的 $(mask, submask)$ 对的数量就有 $3^N$ 种,所以我们最终的复杂度就是 $\mathcal{O}(3^N)$ 级别的。如果你前面预处理了得分,还需要加上预处理的复杂度。
一开始枚举子集常数比较神奇,1800ms 给卡过去了,看了看提交怎么有 103ms 的,然后抄了个没见过的子集枚举方法:
| |
然后做操作就可以了,最后跑了个 98ms。
V. Subtree
树形 DP 换根法转移。完全不会,写了一晚上。
设 $\text{dp}[v]$ 为以 $v$ 为根的答案,容易得到 $\text{dp}[v] =\prod_{u\in\text{son}(v)}\text{dp}[u]$。而对每个节点做一次 DP 复杂度显然是 $\mathcal{O}(N^2)$ 的,显然无法承受,考虑优化。
换根法的题目一般询问的是每个节为根时候的性质(如 POJ 3585,以每个节点为源点的最大流)。
由于给定的是一棵树,我们根据树的性质显然可以导出,每个节点只和自己的子树有关。而另一个好性质是,当我们做一次 dfs 的时候,我们可以发现,每个节点会保存自己所有子树的答案,而真正的答案与这个部分答案的唯一差距就在这次 dfs 过程中的从父亲过来的这条边。
所以,通常我们的换根法是这么做的:
- 以任意节点为根,做一次自底向上的 DP。
- 从根节点出发,做一次自顶向下的 dfs,更新每一棵子树的答案。
而在这个过程中有一个显而易见的观察:对于更新过程 $u\to v$,我们 dfs 过程中更新了 $\text{dp}[u]$,那么当我们更新 $\text{dp}[v]$ 的时候自然需要的是 $v\to u$,这里的问题就在于如何删除 $u\to v$ 的影响,进而再更新答案。这里不同题目的处理方法不同,比较灵活。
那么懂了换根法其实很简单,首先就是 dfs 下去得到任意根的答案,这个 DP 过程应该是显然的,然后是第二次的 dfs 更新答案。
设在第一次扫描过程中节点 $u$ 的 答案为 $f[u]$,显然,对我们选择的任意根 $\text{rt}$,有 $\text{dp}[\text{rt}]=f[\text{rt}]$。设每个节点的更新值为 $g[u]$,则 $g[\text{rt}]=1$ 也是显然的。
接下来考虑任意节点 $v$,假设为 $u$ 的儿子,则容易得到下面的方程: $$ \text{dp}[v]=f[v]\cdot g[v] $$ $f[v]$ 在第一层 DP 过程中得到了,而 $g[v]$ 是多少?由于我们已经知道了根的答案,所以我们要取消当前节点对根答案的影响,这个贡献显然是 $f[v]+1$,而根节点此时为白色也是正确的答案,所以最后要加上 $1$ 来把贡献值调整正确。
所以,$g[v]$ 的值应该是: $$ g[v]=\frac{\text{dp}[u]}{f[v]+1}+1 $$ 那么再把式子完全打开就能得到: $$ \text{dp}[v]=f[v]\cdot(\frac{f[u]\cdot g[u]}{f[v]+1}+1) $$ 发现由于我们自顶向下更新,$f[u],g[u]$ 已知,记录一下 $g[v]$ 然后直接更新 $\text{dp}[v]$ 即可。总复杂度 $\mathcal{O}(N)$。
这题另一个大坑是 $M$ 不一定是个质数,而且还不能保证和答案互质,就不能直接求逆元。处理方法就是,在第一次 dfs 的是时候记录前缀后缀积,转移的时候直接从里面查出来缺项积再做乘法来避免了除法取模。
W. Intervals
很漂亮的一道题。
令 $\text{dp}[i]$ 为当 $s[i]=1$ 时 $1\sim i$ 的答案,显然:
$$ \text{dp}[i]=\max_{1\le j<i\land\forall p,i\in [l_p, r_p], j\notin[l_p,r_p]}\{\text{dp}[j]+\sum{a_p}\} $$
容易发现这是个 $\mathcal{O}(n^2)$ 的过程,肯定是过不去的。观察到转移方程类似于 Q,提示我们用线段树优化转移。
这个题的树上维护有点讲究,我们不考虑只维护 $\text{dp}[j]$,反过来我们考虑维护 $\text{dp}[j]+\sum_{p}$ 全体。容易观察到,当我们进入了某一个线段之后,假设当前为 $1$,那我们对这个线段左端点之前的 $\text{dp}[j]$ 都有贡献,我们直接把贡献加上去;而当我们离开这个线段之后,我们对前面所有左端点的贡献都没有了,所以要取消掉这个贡献。在这种情况下,$\text{dp}[i]$ 的答案显然就是 $\max_{j=1}^{i-1}\{\text{seg}[j]\}$。
所以,我们直接在线段树上维护 $\text{dp}[j]+\sum_{p}$,每次我们进入一条线段时对 $1\sim l_i-1$ 加上 $a_i$,而离开一条线段时对 $1\sim l_i-1$ 加上 $-a_i$,把贡献取消掉。当一轮更新结束之后,直接查询 $1\sim i$ 的值并插入到线段树的此位置即可。最后的答案就是全体最大值。
容易观察到每一条线段只会加一次删一次,所以总复杂度是 $\mathcal{O}(N\log N)$ 的。$N$ 有点大而且操作还是比较多的,所以常数比较大,跑的不是很快。
X. Tower
根据题意显然易得从上往下放更容易考虑。
这道题用到的技巧叫做 Exchange Arguments,我不知道中文应该翻译成什么就保持原名了。
这个技巧通常用于贪心中来证明我们的贪心解就是最优解。而在 DP 中,我们通常使用它来贪心证明 DP 选择的步骤具有某种全序关系,进而利用这个全序关系进行 DP。
假定我们存在某一个贪心解 $G=\{g_1, g_2,\cdots,g_n\}$,而最优解为 $O^*=\{o_1, o_2,\cdots,o_n\}$。假设最终的解可以用一个序列 $S=s_1,s_2,\cdots,s_i,\cdots,s_j,\cdots$ 来描述。我们现在选择某一对参数 $s_i$ 和 $s_j$ 来交换,产生一个新解 $O^*_1$,使得这个新解满足两个性质:
- $O^*_1$ 不比 $O^*$ 更差,或者说至少一样好。同样的,$O^*_1$ 也是一个最优解。
- $O^*_1$ 比起 $O^*$ 更和 $G$ 相似。
那么同样的,我们可以进一步迭代 $O^*_1$ 得到 $O^*_2$。在有限步迭代之后,我们得到了 $O^*_n=G$。我们也就证明了 $G$ 也就是最优解。
用一些更感性的说法来说,始终考虑我们存在某一个解,我们来证明任意一对相邻的元素应该具有某一种序才能保证其中某一项在前时的答案更优。这个显然针对任意一对非相邻的都成立,因为我们证明的是一个全序,总可以在有限次交换内交换为相邻的一对,然后把这对元素排序后再有限次交换回原位置,所以结果始终成立。
那么我们根据题目讨论任意答案塔上的两个砖块 $i$ 和 $j$。假定我们交换他们俩,那么他们上面的重量不会变,设为 $w$,他们下面一块砖的总承重也不会变;同样的,给到这个塔的总价值贡献也不会减少。
那么,唯一影响这两块砖摆放顺序的就是以下两个结论:
- $i$ 放在 $j$ 上塔不会崩溃:$w+w_i\le s_j$
- $j$ 放在 $i$ 上塔一定会崩溃:$w+w_j>s_i$
整理式子,容易得到:$s_j-w_i\ge w> s_i-w_j\implies s_j+w_j>s_i+w_i$,也就是说,$s+w$ 越小的越应该放在上面。所以根据结论,我们按照 $s+w$ 的顺序排个序然后直接跑 0-1 背包即可,复杂度 $\mathcal{O}(N\cdot\max\{s\})$。
Y. Grid 2
由于 $2\le H,W\le 10^5$,之前的 $O(HW)$ dp 显然不可能了;而 $1\le N\le3000$,显然提示我们应该做一个和 $N$ 有关的 dp。
首先的一个观察是我们总是从左上角去右下角,提示我们应该按点的左上角到右下角的顺序来 dp。考虑两个点 $A$ 和 $B$,其中 $A$ 在 $B$ 的左上角。设 $\text{dp}[p]$ 为不经过点 $p$ 左上角所有点从起点到点 $p$ 的路径方案数,我们来考虑从左上角不经过任何点到 右下角的方案数。容斥一下,我们到右下角有四种走法:
- 不经过 $A,B$ 到右下角;
- 只经过 $A$ 到右下角;
- 只经过 $B$ 到右下角;
- 经过 $A, B$ 到右下角。
只经过 $B$ 到右下角很好想,只需要不经过 $A$ 到 $B$ 然后再从 $B$ 到右下角即可。只经过 $A$ 到右下角呢?这一部分会包含经过 $A, B$ 到右下角的方案数,这就提示我们,是否可以不计算第四部分,直接计算减掉第二部分即可?当然可以!
所以,我们的 dp 过程很简单,首先计算出从左上角到 $A$ 不经过其他点的方案数,然后从左上角到 $B$ 的方案数减掉不经过左上角所有点经过 $A$ 到 $B$ 的方案数(这时我们就得到了不经过 $A$ 从左上角到 $B$ 的方案数),最后从左上角到右下角的方案减掉不经过左上角所有点经过 $A$ 到右下角的方案和不经过左上角所有点经过 $B$ 到右下角的方案数。左上角有多个点的情况就留作习题了 :)。
至于代码实现就简单了:我们先排好序然后从左上角的点开始迭代,如果点 $i$ 在点 $j$ 的左上角,我们就在从 $\text{dp}[j]$ 减掉 从起点经过 $i$ 到 $j$ 的方案。显然,转移的方案数就是从左上角不经过其他点到 $i$ 的方案数乘上 $i$ 到 $j$ 的方案数。那么就有:
$$ \text{dp}[j]=\binom{P_j.x+P_j.y}{P_j.x}-\sum_{\forall i, P_i.x\le P_j.x, P_i.y\le P_j.y}\text{dp}[i]\cdot\binom{P_j.x+P_j.y-P_i.x-P_i.y}{P_j.x-P_i.x} $$
提前把右下角这个点 $(H,W)$ 添加进去先排个序再一起 dp,答案就是 $\text{dp}[N]$,复杂度为 $\mathcal{O}(N\log N+N^2)$。写出来其实挺短的。
Z. Frog 3
斜率优化或者李超树优化。又到了现学现卖的时间了啊。
先分析题目,类似于原题,我们很容易写出转移方程: $$ \text{dp}[i] = \min_{1\le j<i}\{\text{dp}[j]+(h_i-h_j)^2+C\} $$ 拆一下式子,我们进一步写一下: $$ \text{dp}[i] = h_{i}^2+C+\min_{1\le j<i}\{\text{dp}[j]+h_j^2-2h_ih_j\} $$ 我们可以发现,对于某个 $j$,$\text{dp}[j]$ 和 $h_j$ 都是确定的,那么就变成了,对于某个确定的 $i$,我们需要找到前 $j$ 个值中最小的值。我们观察这个式子,重写一下:$v=-2h_ih_j+\text{dp}[j]+h_j^2$,可以发现,$v$ 是一条直线,仅和 $h_i$ 有关。所以,我们就变成了在前 $j$ 条直线中,对于确定的 $h_i$,找到这样的一条直线,使得 $v$ 最小。我们现在来看怎么处理这个问题。
斜率优化英文名叫 Convex Hull Trick (CHT)。发现有凸包没有?这个优化的核心就在理解这个凸包上。
实际上,这个过程我们需要的不是一个凸包,而是凸壳。让我们先来观察一下这个图:
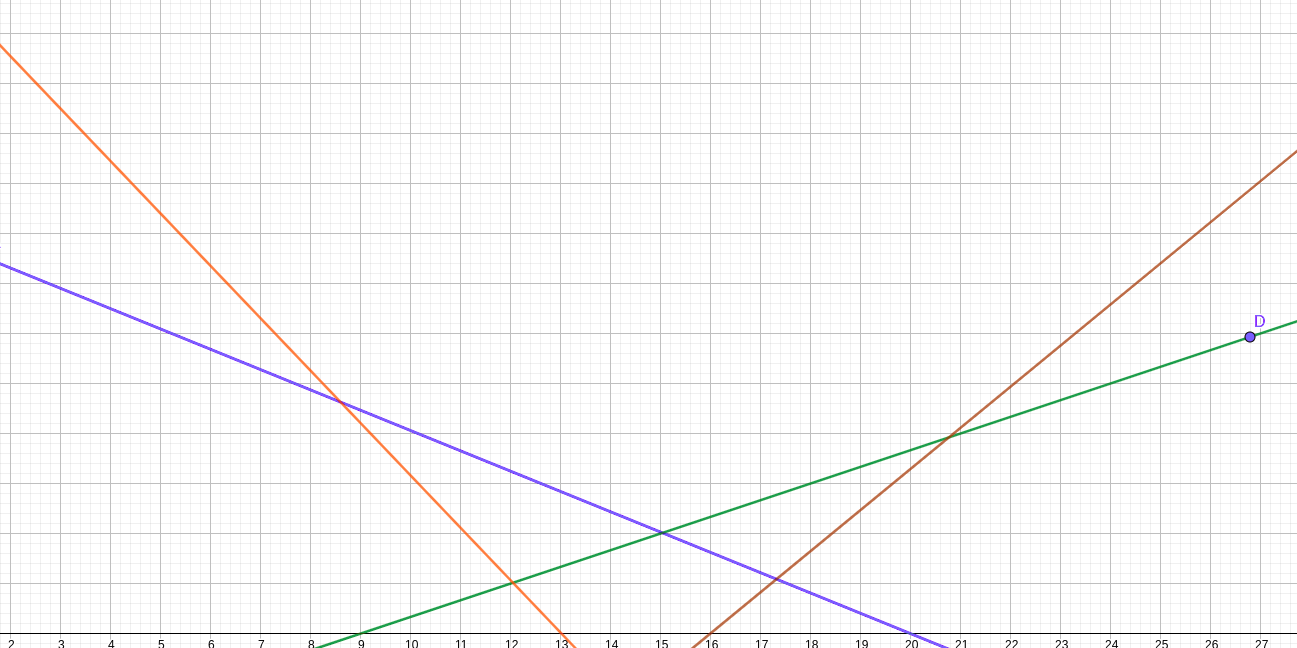
答案会在什么位置?显而易见的是,都在“最上面”的直线上。什么叫最上面呢?对于一个确定的 $x$,一定在所有交点的最上面。现在,我们来观察一下这几条直线构成的凸壳:

发现什么没有?所有可能的答案都在这个凸壳的边界上!这就是斜率优化的本质:维护这样的一个凸壳的集合,保证我们的查询能够落在的任何一条直线都在这个凸壳上。
显而易见的是,如果要维护这个凸壳,我们自然需要一个比较好的数据结构。我们现在来考虑这个数据结构的实现(我们假定插入直线的顺序按斜率有序插入,同时也假定查询的点按顺序是有序的):
- 询问:我们从最左侧的直线开始比较,假如 $y_0 < y_1$,说明答案不在这条线上,删除,然后重复上述过程,直到找到答案,直接返回。
- 插入:考虑最右侧的直线,如果我们插入的这条直线和最右侧直线的交点在最右侧直线和它左侧直线交点的左侧,那么就考虑把这条直线删除。
观察到什么没有?由于上面的所有操作都只涉及一端,我们完全可以使用一个双端队列来维护它!
正确性也是显然的:
- 询问:由于查询会一直往左侧靠近,答案不会再出现在右侧,所以这个过程正确。
- 插入:由于查询是往左侧靠近的,答案不会再落在右侧,虽然原始直线交点右侧比插入的直线更高,但是答案不会出现在那一侧;而对于交点左侧,插入的直线比原始直线更高,答案会落在新直线上。所以原始直线可以被删除,则这个过程也正确。
那么我们的 CHT 就写完了!
我的实现可以参考这里。由于每条直线只会至多被插入和删除一次,则总复杂度就是 $\mathcal{O}(n)$ 的。
而实际上全动态的 CHT 写起来比较麻烦,不如李超树好写,所以这个情况最好写的还是在斜率有序的情况下。
为什么叫李超树呢?因为是李超的 线段树 ppt 里面提到的建树方法(
李超树就是一棵简单的线段树而已,区别是维护的东西不同,李超树维护的东西叫做“优势线段”。什么是优势线段呢?某个区间内从上往下看长度最长的线段。例如,下图中的红色线段就是当前区间中最长的优势线段。
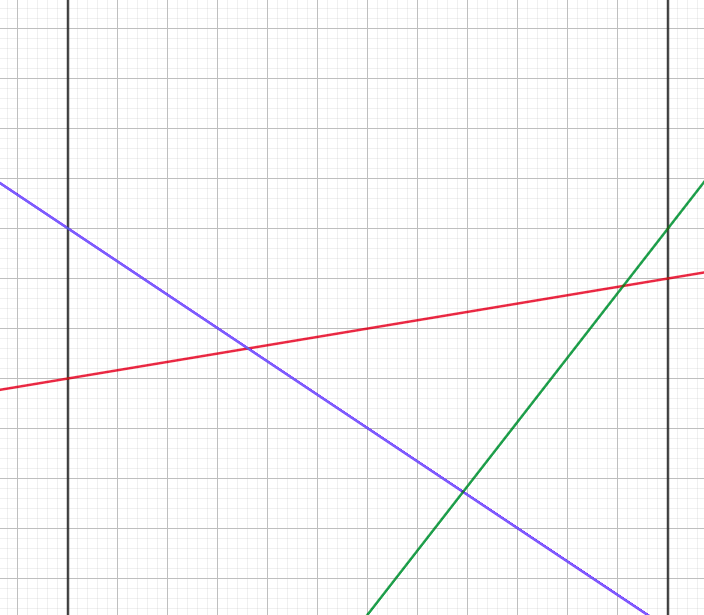
考虑上面的斜率优化的讨论,我们可以发现,这样维护出来的线段集合就正好在答案区间内构成了一个凸壳!所以显而易见,这是正确的。
接下来我们考虑怎么维护这些线段。首先是添加过程:
- 假设当前区间没有线段:直接添加
- 假设新线段比旧线段有优势:新线段替换旧线段,然后带着旧线段继续更新
- 假如有交点:讨论交点位置,并把当前线段带到另一侧更新
观察上面的图,发现假如我们讨论当前区间,并不一定能获得最大值,因为可能最大值在绿色线段上,这样的话我们是得不到答案的,所以查询的时候不能直接返回当前区间的值,我们需要一路走到叶子节点,这里面的最大值才是答案。
容易观察得到,插入就是简单的线段树插入,而查询需要一次完整的走树,所以总复杂度是 $\mathcal{O}(n\log^2 n)$。
我的实现可以参考这里。
回到本题,实际上我们只需要维护直线 $-2h_ih_j+\text{dp}[j]+h_j^2$ 的值即可。具体这么做:
- 首先把第一条直线 $-2h_1x+h_1^2$ 插入进去。
- 依序更新每一条线段,首先查询出当前的最小值 $m$,则 $\text{dp}[j]=m+h_j^2+C$ 之后把新的线段 $-2h_jx+\text{dp}[j]+h_j^2$ 插入进去。
答案就是 $\text{dp}[N]$。根据选择的结构不同,复杂度也不一样。