最近做的题 ver 2019.12

弹指一挥间实习五个月了，虽然经常很忙，但偶尔也能抽出时间想一想做几个题。感觉最近也比较摸，不记一下真就快忘光了，还是写一下实习以来做的题的简单题解，防止手生吧。

Codeforces 1265E

期望 DP。话说回来我期望 DP 好像没做过几个题，感觉还是不大懂，有机会补一下。

题目很简单，Cretnx 面前有 $n$ 面镜子，每天会有 $p_i$ 的概率通过这面镜子，有 $1-p_i$ 的概率无法通过。通过了镜子第二天前往下一面镜子，没通过则回到第一面镜子，问通过所有镜子（最后一面镜子也得通过，相当于到达不存在的第 $n+1$ 面镜子）的期望天数。

考虑每面镜子是一个点，每个点有 $p_i$ 的概率转移到下一个点，有 $1-p_i$ 的概率回到第一个点，那就变成了一个常见的模型：有向图路径长度期望 DP。

我们同样设计状态：假定最终目标是点 $n+1$，$f_i$ 定义为从点 $i$ 出发到 $n+1$ 这个点的期望天数，那么我们倒序 dp，答案就是 $f_1$，$f_{n+1}=0$。类比有向图的转移方程，我们很容易写出来现在转移方程： $$ f_i = p_i f_{i+1}+(1-p_i)f_1+1 $$ 解释应该是很简单的，我们从点 $i$ 出发，有 $p_i$ 的概率走到下一个点，有 $1-p_i$ 的概率返回第一个点，那么我们期望到终点的天数就是这两种情况之一。而我们怎么选都要多一天，所以要加 1。

这个转移也可以通过全期望公式 $E(X) = E[E(X|Y)]$，那么就是给定我到了点 $i$，前往后两个点的期望的和，根据线性性，1 被提出来，答案符合上式。

但是很尴尬的是，我们看 $f_1=p_1f_2+(1-p_1)f_1+1\implies f_1=f_2+\frac{1}{p_i}$。嗯？我们所有的递推式都需要 $f_1$，但是 $f_1$ 依赖了 $f_2$，这不就循环依赖了，高斯消元？

让我们再推几个式子：$f_1=f_3+\frac{1}{p_1p_2}+\frac{1}{p_2}$，$f_1=f_4+\frac{1}{p_1p_2p_3}+\frac{1}{p_2p_3}+\frac{1}{p_3}$，……

最终我们极易得到 $f_1=f_{n+1}+\sum_{i=1}^n\prod_{j=1}^i\frac{1}{p_{n-i+1}}$。注意到 $f_{n+1}=0$，这个题就做完了。把所有值读进来然后倒序求一个倒数后缀积就行，逆元需要注意一下，复杂度 $\mathcal{O}(n)$（求逆元是个常数）。

SPOJ KGSS

给定 $n$ 长度的序列 $\{a_i\}$，$q$ 次操作，处理下面两种事件：

• 更新 $a_i$ 的值为 $x$。
• 求 $\max\{a_i+a_j\}, i\ne j, i, j\in[l, r]$。

这种一眼看出来就是线段树，第二个操作显然是区间最大和区间次大，然后第一个事件只有单点修改还不传标记，维护难度大大降低。

这个题区间次大的维护有点说法，考虑左右两个区间的值合并，你有四个数，四个数里面求一个最大和求一个次大然后更新当前节点，查询的时候也是查出来四个数再合并。注意到对于某个点我们只有一个值，不存在次大，所以某个点的次大值应该是 $-1$ 而不是这个值本身。然后这个题做完了。

Project Euler 183

定义 $P(n,k)=(\frac{n}{k})^k, k\in\mathbb{N}^+$，$M(n)=\max P(n,k)$，$D(n) = n$ 如果 $M(n)$ 是一个有限小数，否则 $D(n)=-n$，求 $\sum_{n=5}^{10000}D(n)$。

看看 $P(n,k)$，掏出来 WolframAlpha，立即可得 $k=\frac{n}{e}$ 时最大，即 $M(n)=P(n, \frac{n}{e})=e^{\frac{n}{e}}$。然后呢，这东西是不是有限小数怎么整？

注意到要求，我们可以确定 $k$ 是最接近 $\frac{n}{e}$ 的整数，另一个观察是，有限小数的有限倍幂一定是有限小数。所以，我们问题就变成了求 $\frac{n}{k}$ 是不是有限小数了。 假设它是，则考虑小数形式下共有 $d$ 位，则乘 $10^d$ 次方一定为一个正整数，也就意味着 $k|(10^d\cdot n)$。我们对分子分母求一下 $\gcd$，易得 $k=2^{\alpha}5^{\beta}p$，则一定有 $p|n$。所以，我们贪心的干掉 $k$ 里面的 $2$ 和 $5$ 因子，再判断一下最后结果能不能被 $n$ 整除就可以了。

Codeforces 77E

学了个新科技，圆的反演变换。具体怎么反演的网上应该有很多教程，找个博客看看就行，还是挺简单的。

题意比较清晰，给定一个大圆和两个小圆，两个小圆在大圆内部，三圆圆心共线且两两相切，问往第二个小圆上方不断添加与第一个小圆，外侧大圆以及前一个圆相切的圆，第 $n$ 个圆的半径是多少。

直接以第一个小圆和外侧大圆切点为反演中心，任意反演半径反演三个圆，极易画出下面的图：

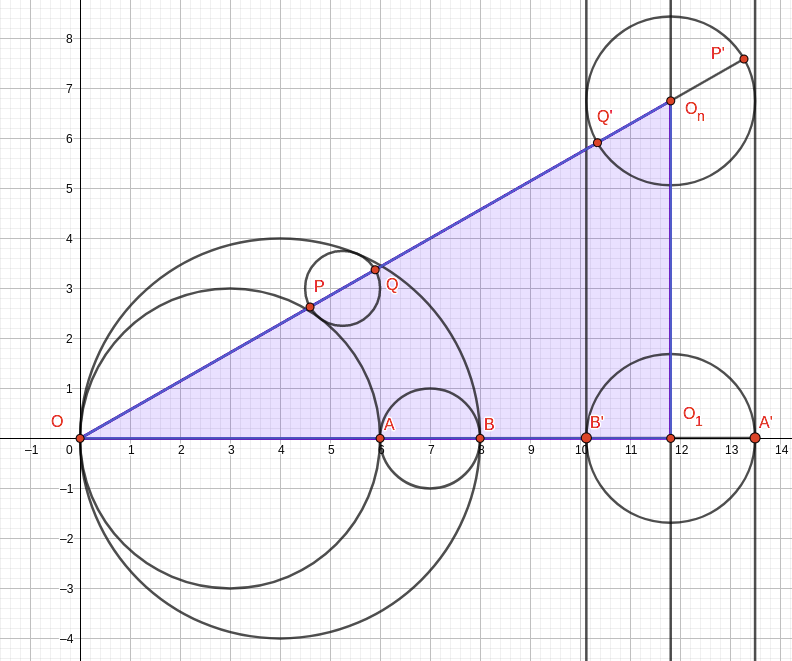
假设反演半径为 $1$，那么很容易得到 $|OA|\cdot|OA’| = |OB|\cdot|OB’|=1$，极易解出 $|OA’|$ 和 $|OB’|$。设反演后的圆半径为 $r’$，则 $r’=\frac{|OA’|-|OB’|}{2}$。然后就能得到 $|OO_1|=|OB’|+r’$，而 $|O_1O_n|=2nr’$，则 $|OO_n|$ 就很好求了，勾股定理一下。之后立刻就有 $|OP’|=|OO_n|+r’, |OQ’|=|OO_n|-r’$，按照 $|OP|\cdot|OP’|=|OQ|\cdot|OQ’|=1$ 反演出来 $|OP|$ 和 $|OQ|$，那么第 $n$ 个圆的半径就是 $\frac{|OQ|-|OP|}{2}$，这个题就做完了。每个圆求解只需要 $\mathcal{O}(1)$，所以总复杂度 $\mathcal{O}(t)$。

要注意反演圆的圆心不是原先圆的圆心反演，这个东西我上来以为是对的然后推了三个式子发现各自不等啊，直接拉闸。

还有个后续题，HDU 6158，其实就是同样的过程然后反演一下就行。选个合适的反演半径化简一下式子，然后注意到不需要枚举到 $n$，枚举到对答案没有贡献即可。注意一下精度就变成套路了。

杂题

• HihoCoder 1142：我没写过三分，都是我队友写的，所以我也写一下三分。我写了，一发 A 了，有什么好说的？

• Project Euler 258：给定 $$ \begin{cases} f_i=1,&0\le i\le1999 \\f_i=f_{i-2000}+f_{i-1999},& 2000\le i \end{cases} $$ 求 $f_{10^{18}}\ \text{mod}\ 20092010$。有经验的选手肯定就是一个 $\mathcal{O}(k^3\log n)$ 的矩阵快速幂，然后发现 $k=2000$ 拉闸。
  这个题标准做法是用 Cayley-Hamilton 定理优化线性递推成一个 $\mathcal{O}(k^2\log n)$ 的过程再求。我在这里写不是因为我会这个方法，而是我去搜了一个 dls 的 BM 板子，枚举了 4000 项一发就莽过去了。 这件事教育我们，出题不要出线性递推，不然你死都不知道怎么死的。